微分方程式の応用
obj0001.png
コンデンサの過渡現象とラプラス変換
起電力E、抵抗R、自己インダクタンスL、静電容量Cの
右の回路の過渡現象を解いてみましょう。
キルヒホッフの法則から回路方程式は以下の
ようになります。
コンデンサにたまっている電荷量をQ(t)とします。
電流と電荷の関係から
I(t)=
dQ(t)
dt
R=50[Ω]
従って抵抗での電圧降下は以下のようになります。
L=0.65[H]
C=22[μF]
RI=R
dQ(t)
dt
E=5[V]
自己インダクタンスでの電圧降下は以下のようになります。
L
dI(t)
dt
 =L
d
2
 Q(t)
dt
2
コンデンサでの電圧降下は
Q(t)
C
 です。
従って以下の方程式が得られます。
E=R
dQ(t)
dt
 +L
d
2
 Q(t)
dt
2
+
Q(t)
C
ここでコンデンサでの時刻t=0での容量は０とします。
初期条件
Q'(0)=0
Q(0)=0
Laplace変換技法を使ってこの微分方程式を解いてみましょう。
pfrm0001.png
関数定義
pfrm0002.png
pfrm0003.png
従って
Rs
ℒ
{Q(t)}+Ls
2
ℒ
{Q(t)}+
1
C
ℒ
{Q(t)}=
E
s
この式を
ℒ
{Q(t)}で解く
ℒ
{Q(t)}をTと置く
方法
RsT+Ls
2
 T+
1
C
 T=
E
s
これをカルキングの方程式（一元多項式の記号解）で解くと以下になる。
T=
1
Rs+Ls
2
 +
1
C
E
s
 =
CE
CLs
3
 +CRs
2
 +s
従って
ℒ
{Q(t)}=
CE
CLs
3
 +CRs
2
 +s
この両辺に逆Laplace変換すると
だから
ℒ-1
{
ℒ
{Q(t)}}=Q(t)
Q(t)=
ℒ-1
CE
CLs
3
 +CRs
2
 +s
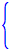
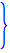
ここで記号式のままでは逆Laplace変換は求まりません。ここでは以下の値で
解いてみます。
R=50[Ω]
L=0.65[H]
C=22[μF]
E=5[V]
しかし単位が付いたままでは解けません。そのため標準単位で求め無単位化する。
Cの部分は以下のようにしてF単位にできます。
これをいったん代入します。
C=22[μF]
このようにして単位を指定して計算します。
C=[F]
C=0.000022[F]
このような準備して下記の4つの単位部を除いた式を「代数代入《する。
代入定義（数値モード）ではなく代数代入するのは、後で代数計算で参照するためです。
R=50
L=0.65
C=0.000022
E=5
この値を使って
CE
CLs
3
 +CRs
2
 +s
 =
0.00011
0.0000143s
3
 +0.0011s
2
 +s
代数計算
以下の記号処理（代数計算、代数代入）での計算精度は６桁にしています。
逆Laplace変換を求めるに先だって必ず部分分数分解をする必要があります。
pfrm0004.png
プロパティ
代数計算
精度6桁
故に得られた解は以下の通りになる。
pfrm0005.png
pfrm0006.png
Q(t)を関数定義する。
Q(t)=-0.00011e
-38.4616t
 cos(261.631t)-0.0000161707e
-38.4616t
 sin(261.631t)+0.00011
初期値の確認
代入
t=0
Q(0)=0
計算
Q'(0)=0　　の確認
Qの一階微分の関数を求める
dQ(t)
dt
 =0.0000000195883e
-38.4616t
 cos(261.631t)+0.02940136099512e
-38.4616t
 sin(261.631t)
この関数を使ってt=0での値を求める。
0.0000000195883e
-38.4616t
 cos(261.631t)+0.02940136099512e
-38.4616t
 sin(261.631t)=0.0000000195883
0に近い
微分方程式の検算
R
dQ(t)
dt
 +L
d
2
 Q(t)
dt
2
+
Q(t)
C
 -E=0.000000350741e
-38.4616t
 cos(261.631t)-0.00000230055e
-38.4616t
 sin(261.631t)
0に近い
有効桁数６桁で解いているので少し誤差が出ます。