ラプラス変換、逆ラプラス変換
「カルキング10プロフェッショナル版《で作成
y を 仮想関数として定義
y(t)=Æ
{y'
(t
)}+
{2y
(t
)}=
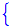 e
e
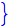
(1)
ラプラス変換を実行 (代数計算を実行)
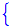 e
e
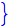
=
以上により方程式(1)は
となる
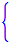
y(t)
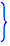
=sY-y
(0
)
(
Y = y ( t )
を表しています )
ラプラス変換の微分機能により
この方程式を記号解で解くと
また y(0)=3より方程式(2)は
この解の右辺に対して「部分分数分解《を行う
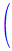
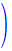
=
+
従って
{
{y(t)
}}=
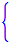
+
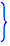
y(t)=
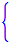
+
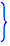
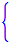
+
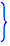
=
e
+2
e
逆ラプラス変換の実行(代数計算)
得られた最終解
フーリエ展開をスクリプトで作成する
f
(x
) =
+
(a
cosnx + b
sinnx)
f (x) = x
例題1
FourierExpansion( f,"x",10 )=+2.0000sinx-1.00002sin2x
+0.66674sin3x-0.50018sin4x+0.40036sin5x-0.33397sin6x
+0.28676sin7x-0.25161sin8x+0.22460sin9x-0.20339sin10x
この式をグラフにすることもできる




