上完全楕円積分
上完全楕円積分は色々な表記方法があり最新の注意が必要です。
カルキングでは3通りの定義に基づく表記法を用意しています。
引数の区切り記号に注意してください。
区切り記号を別の区切り記号に変更しないでください。
同じ関数吊Fを使っていますが、内部表現は全て異なっています。
（注：書籍によっては上完全楕円積分と言わずに単に楕円積分ということも
あります。）
第一種上完全楕円積分
f :実数
F
(f ,k )=
ó
ô
õ
f

0
1
Ö(1-k
2
 sin
2
 q)
 dq
k：複素数
t = sin θ x = sin φ
F
(x ;k )=
ó
ô
õ
x

0
1
Ö(1-t
2
 )(1-k
2
 t
2
 )
 dt
F
(f \a )=
ó
ô
õ
f

0
1
Ö1-(sinasinq)
2
dq
計算例
F
(0.3 ,0.8 )=0.302902599898209
同じ引数値を与えても以下のようにセミコロン区切りの関数の計算値は異なります。
F
(0.3 ;0.8 )=0.307734343459238
同じ計算値を得るためには以下のようにsin関数の操作が必要です。
F
(sin(0.3) ;0.8 )=0.302902599898209
; タイプのFを基準に考えると計算が違うため、以下のように sin
-1
  の操作が必要になります。
F
(0.6 ;0.8 )=0.67290466152868
F
(sin
-1
 (0.6) ,0.8 )=0.67290466152868
F
(0.3 \0.5 )=0.301025197178559
高精度計算例
F
(0.3 ,0.8 )=0.30290259989820913986211978000244501460759712
96428158063403187263003949941849326229592556905485006296
k が複素数の時の高精度計算例
F
(0.3 ,0.8+2.5i )=0.2781646657744814639605835133721286148056
90285480551370608928240399336192965646169922087403449515
3509 + 0.0120351926018352496270005406417875431919943700644
8209542896176639468589839027569973965304467627338854i
以下のような定義が使われることがあります。
カルキングでは｜区切り記号は第一種では使いません。
F(f|m) =
ó
ô
õ
f

0
1
Ö(1-msin
2
 q)
 dq
m=k
2
   として
F
( f,k
2
  )を代わりに使ってください。
第ニ種上完全楕円積分
f :実数
E
(f , k )=
ó
õ
f

0
Ö(1-k
2
 sin
2
 q)dq
k ：複素数
t = sin θ x = sin φ
E
(x ; k )=
ó
ô
õ
x

0
Ö1-k
2
 t
2
Ö(1-t
2
 )
 dt
E
(f \ a)=
ó
õ
f

0
Ö1-(sinasinq)
2
 dq
引数の区切り記号の扱いは第一種上完全楕円積分に準じます。
計算例
E
(0.3,0.5)=0.298891411016533
E
(0.3 ;0.5 )=0.30353176542728
E
(0.3 \0.5 )=0.298981042078219
高精度計算　　　　　注：多少時間がかかります。
E
(0.3,0.5)=0.298891411016498599402892475401513242147503791
9047057323551755572732533207493080133363262397718306257
高精度複素数計算　　　　　注：多少時間がかかります。
E
(0.3,0.5+2i)=0.3160087094185091846211703233409100502770408
9044362 - 0.0080851753921253815044382902927218151899007353
402698i
第三種上完全楕円積分
Π
(n ;f ,k )=
ó
ô
õ
f

0
1
Ö(1-k
2
 sin
2
 q)(1-nsin
2
 q)
 dq
n , f , k：実数
Π
(n ;f |m )=
ó
ô
õ
sin f

0
1
1-nt
2
1
Ö(1-t
2
 )(1-mt
2
 )
 dt
Π
(n ;f \a )=
ó
ô
õ
f

0
1
1-nsin
2
 q
1
Ö1-(sinasinq)
2
dq
計算例
Π
1
3
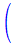
  ;π/5 , Ö0.3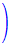=0.668734807465291
Π
1
3
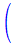
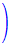
  ;π/5 | 0.3=0.668734807465291
Π
(-0.7 ;0.6 \0.5 )=0.565666453272373
解説書の中には以下のような定義がされている場合もあります。
P(n,x,k)=
ó
ô
õ
x

0
1
1-nt
2
1
Ö(1-t
2
 )(1-k
2
 t
2
 )
 dt
x=sin f
k=Öm
このように x , k を定義して、P(n,x,k)を計算すれば、
Π
(n ;f |m )と同じ解になります。
例
n=
1
3
f=
π
5
m=0.3
Π
(n ; f| m)=0.668734807465389
このようにx,kを定義すると
x=sin f
k=Öm
ó
ô
õ
x

0
1
1-nt
2
1
Ö(1-t
2
 )(1-k
2
 t
2
 )
 dt=0.668734807465333
（この定積分の精度の限界で完全には一致していません。）