極座標変換への微分応用
地球の運動方程式を解くときには、x-y座標よりも
極座標系の方が、微分方程式を解くときに便利です。
この計算は通常、手計算で行いますが結構複雑です。
ここでは、カルキングの記号計算を使って、
r方向、θ方向の加速度成分を求めてみます。
ただし一部は手計算が必要になりますが、全て
手計算するよりもはるかに便利です。
記号計算機能だけでなく、カルキングの数式置換機能も利用します。
応用上の基本は、
,
,
,
,
,
,
を利用することです。右肩の(1),(2)は文字修飾です。
通例、右肩の(1),(2)は微分階数を表しますので、この類推からこの吊前にしました。
x=rcosq
y=rsinq
仮想関数定義する
r(t)=Æ
q(t)=Æ
手入力
カルキングでの記号計算
=
=
(rcos
q)=-r
sin
q+
cos
q
したがって
(1),(2)に対して置換表を適用すると以下のようになる
仮想関数定義
代数代入定義
代数計算
因数分解
手計算
↓
↓
↓
=
cos
q
sin
q=
cos
q
sin
q
(cos
q+sin
q)
=
sin
q
cos
q=r
cos
q+r
sin
q=
r(cos
q+sin
q)=
r
したがって
(3),(4)から
代数計算
↓
=
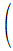
cos
q-
sin
q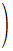
+
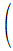
-r
sin
q+
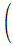
-r
cos
q-
sin
q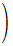
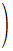
上記の式に、
,
,
,
の置換をすると以下の式になる
=(
cos
q-
sin
q)+(-r
sin
q+(-r
cos
q
sin
q)
)
右辺を代数計算する
(
cos
q-
sin
q)+(-r
sin
q+(-r
cos
q
sin
q)
)
=-r(
)
cos
q
cos
q-r
sin
q
sin
q他方
したがって
同様に
=
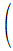
r
cos
q+
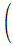
cos
q-
rsin
q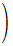
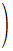
+
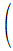
cos
q+
sin
q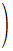
上記の式に、
,
,
,
の置換を施すと以下の式になる。
=(r
cos
q+(
cos
q-
rsin
q)
)+(
cos
q
sin
q)
右辺を代数計算する
(r
cos
q+(
cos
q-
rsin
q)
)+(
cos
q
sin
q)
=r
cos
q
cos
q-r(
)
sin
q
sin
qさらに仮想関数定義を行う
以下の2式を代数代入定義する
=-r(
)
cos
q
cos
q-r
sin
q
sin
q
=r
cos
q
cos
q-r(
)
sin
q
sin
q
他方以下の2式より
=
cos
q
sin
q=-r(
)
cos
q
cos
q-r(
)
sin
q
sin
q
右辺の式を代数計算して簡素化する。
-r(
)
cos
q
cos
q-r(
)
sin
q
sin
q
cos
q
sin
q-r(
)
cos
q-r(
)
sin
q
-r(
)
=
-r
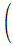
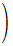
手計算で式の順序を変更する
手計算で式の順序を変更する
同様に
=
sin
q
cos
q=r
cos
q
cos
q+r
sin
q
sin
q
=r
cos
q+r
sin
q
cos
q
sin
q
=r
=r
+2
=
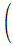
r
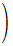
したがって







