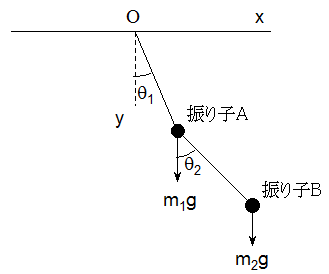
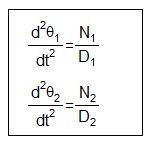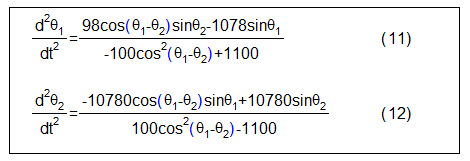2重振り子の微分方程式
2重振り子の方程式はかなり複雑です。
式が長くて、分かりずらいため、
以下のような補助関数を導入します。
添字を多用していますが
これらは、文字修飾での入力です。
(
,
)
sin(
-
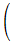
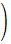
cos(
-
)sin(
-
)
×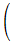
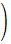 g
sin
g
cos(
-
)sin
g
sin
g
cos(
-
)sin
(
,
)
cos(
-
)sin(
-
)
×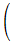
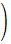
sin(
-
)
×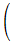
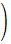 g
cos(
-
)sin
g
sin
g
cos(
-
)sin
g
sin
2重振り子の連立微分方程式は以下になります。
定数変数を以下のように代数代入定義します。
g=9.8
代数計算
代数計算
(
,
)=98cos
(
-
)sin
-1078sin
代数計算
代数計算
(
,
)=-10780cos
(
-
)sin
+10780sin
したがって2重振り子の連立微分方程式は以下になります。
微分方程式では必ず式番号をつけます。
微分方程式諸元表
上記方程式を解くためには必ず微分方程式諸元表を作成する必要があります。
「入力《-「表/行列《-「微分方程式の諸元表《で作成します。
以下はこの表の空欄に必要な初期値をセットしたものです。
initial value2は
,
の t=0 の時の値です。
今回の方程式は、初期値の与え方によって多様なモードの解が得られます。
解法 下記の表を選択して、「実行《*「方程式関連《*「微分方程式《
| indepedent var |
t |
initial value |
0 |
final value |
10 |
| step num |
1000 |
output num |
1000 |
equation num |
2 |
| dependent var |
|
|
|
|
|
| initial value1 |
0.5 |
0.8 |
|
|
|
| initial value2 |
0.0 |
10.0 |
|
|
|
| expression id |
(11) |
(12) |
|
|
|
,
のデータ数が多いので、ここでは先頭の100個をそれぞれ表示します。
,
に対応する配列データは
,
にセットされています。
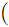
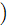
={0.5, 0.49998, 0.49991, 0.4998, 0.49965, 0.49945, 0.49921, 0.49893, 0.49861, 0.49824, 0.4
9782, 0.49737, 0.49686, 0.49631, 0.49572, 0.49508, 0.49438, 0.49365, 0.49286, 0.49202, 0.49113, 0.4
9019, 0.4892, 0.48817, 0.48708, 0.48594, 0.48475, 0.48351, 0.48223, 0.48089, 0.47951, 0.47808, 0.47
661, 0.47509, 0.47353, 0.47193, 0.47028, 0.46859, 0.46687, 0.4651, 0.46329, 0.46144, 0.45955, 0.457
62, 0.45565, 0.45365, 0.4516, 0.44951, 0.44738, 0.44521, 0.443, 0.44075, 0.43845, 0.43611, 0.43372,
0.43129, 0.42882, 0.4263, 0.42374, 0.42113, 0.41848, 0.41578, 0.41305, 0.41026, 0.40744, 0.40458, 0.
40168, 0.39874, 0.39576, 0.39275, 0.38971, 0.38663, 0.38351, 0.38037, 0.37719, 0.37398, 0.37074, 0.
36747, 0.36416, 0.36083, 0.35745, 0.35405, 0.35061, 0.34714, 0.34363, 0.34008, 0.33651, 0.33289, 0.
32924, 0.32555, 0.32183, 0.31807, 0.31428, 0.31045, 0.30659, 0.30269, 0.29877, 0.29481, 0.29082, 0.
28681}
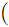
={0.8, 0.89995, 0.99953, 1.0987, 1.1973, 1.2953, 1.3927, 1.4894, 1.5854, 1.6806, 1.7749, 1.
8685, 1.9612, 2.053, 2.144, 2.2341, 2.3233, 2.4117, 2.4993, 2.5861, 2.6722, 2.7575, 2.8421, 2.926, 3.0
094, 3.0923, 3.1746, 3.2566, 3.3382, 3.4195, 3.5007, 3.5817, 3.6627, 3.7438, 3.8249, 3.9063, 3.988, 4.
0699, 4.1524, 4.2353, 4.3187, 4.4027, 4.4875, 4.5729, 4.659, 4.746, 4.8338, 4.9224, 5.0119, 5.1022, 5.
1934, 5.2856, 5.3786, 5.4725, 5.5672, 5.6627, 5.7591, 5.8562, 5.954, 6.0524, 6.1514, 6.2509, 6.3509, 6
.4511, 6.5516, 6.6523, 6.7529, 6.8535, 6.954, 7.0541, 7.154, 7.2533, 7.3521, 7.4503, 7.5479, 7.6447, 7.
7407, 7.8359, 7.9302, 8.0236, 8.1162, 8.2078, 8.2985, 8.3883, 8.4772, 8.5652, 8.6523, 8.7385, 8.824, 8
.9087, 8.9926, 9.0759, 9.1586, 9.2407, 9.3224, 9.4037, 9.4846, 9.5653, 9.6458, 9.7263}
,
が求められましたので、振り子A、Bの座標位置は以下のようになります。
代入定義
=10sin
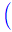
代入定義
=-10cos
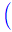
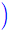
代入定義
代入定義
これらの代入定義は配列になっていることに注目してください。
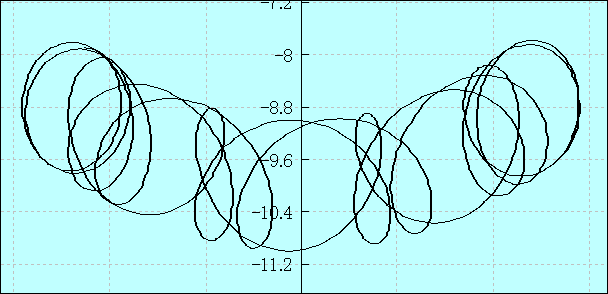
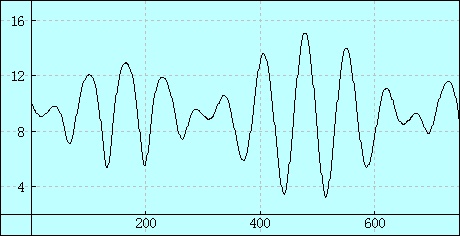
ここでは特に興味深い振り子Bの軌跡を関数グラフで描画してみます。
この配列データを2D*グラフのデータ型(X-Y軸)で描画する。
振り子Bの回転した軌跡のグラフ
の微分の計算値を求めてみます。以下のようにして計算できます。
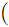
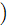
={10, 9.9679, 9.9275, 9.8794, 9.8243, 9.7628, 9.6957, 9.6239, 9.5479, 9.4685, 9.3865, 9.302
5, 9.2171, 9.131, 9.0448, 8.959, 8.8743, 8.7912, 8.7103, 8.6322, 8.5573, 8.4862, 8.4195, 8.3577, 8.301
3, 8.2508, 8.2066, 8.1691, 8.1387, 8.1157, 8.1004, 8.0928, 8.0931, 8.1013, 8.1174, 8.1411, 8.1723, 8.2
107, 8.256, 8.3077, 8.3654, 8.4287, 8.4971, 8.5699, 8.6468, 8.727, 8.8101, 8.8954, 8.9824, 9.0705, 9.1
59, 9.2474, 9.335, 9.4211, 9.5049, 9.5858, 9.6629, 9.7355, 9.8028, 9.8638, 9.9177, 9.9639, 10.001, 10.
03, 10.049, 10.057, 10.056, 10.044, 10.022, 9.9901, 9.9493, 9.8999, 9.8427, 9.7784, 9.7079, 9.6319, 9.
5514, 9.4671, 9.3798, 9.2902, 9.1992, 9.1073, 9.0154, 8.924, 8.8338, 8.7454, 8.6595, 8.5768, 8.4978, 8
.4231, 8.3535, 8.2895, 8.2316, 8.1804, 8.1363, 8.1, 8.0716, 8.0515, 8.04, 8.0371, 8.043, 8.0576, 8.0808
, 8.1123, 8.1519, 8.1991, 8.2537, 8.315, 8.3826, 8.4558, 8.5342, 8.617, 8.7036, 8.7934, 8.8858, 8.98, 9.
0754, 9.1712, 9.2668, 9.3614, 9.4543, 9.5446, 9.6314, 9.7139, 9.7911, 9.8622, 9.9261, 9.982, 10.029, 1
0.066, 10.093, 10.109, 10.114, 10.107, 10.09, 10.061, 10.022, 9.9733, 9.9157, 9.85, 9.7771, 9.6981, 9.6
137, 9.525, 9.4328, 9.338, 9.2414, 9.1439, 9.046, 8.9487, 8.8526, 8.7584, 8.6668, 8.5786, 8.4943, 8.41
46, 8.3403, 8.2719, 8.21, 8.1552, 8.108, 8.0689, 8.0383, 8.0164, 8.0035, 7.9997, 8.0051, 8.0196, 8.043,
8.0751, 8.1157, 8.1642, 8.2202, 8.2832, 8.3526, 8.4277, 8.5081, 8.5929, 8.6816, 8.7735, 8.8678, 8.964
, 9.0611, 9.1587, 9.2559, 9.3519, 9.446, 9.5373, 9.625, 9.7083, 9.7861, 9.8575, 9.9217, 9.9778, 10.025,
10.062, 10.089, 10.105, 10.109, 10.103}
振り子Bの速度を求めてみます。
この式に対してはなにも操作しない
この式に対してはなにも操作しない
仮想関数定義をします。
関数定義
関数定義
θは具体的な関数が定義されていなくても下記のような微分計算ができます
=
(10sin
+sin
)=
cos
+10
cos
代数計算
=
(-10cos
-cos
)=-
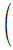
-10
sin
+
sin
代数計算
代入定義
代入定義
代入定義
これをデータ型(Y軸)でグラフ表示すると以下のようになります。
{v}
振り子Bの速度