線形計画法 例題と説明
具体的例題に則して、概要を説明します。
7x+5y+4zの最大値を求める。ただし制約条件式(1),(2),(3)を満たすこと。
ただしx,y,zはかならず0以上であること。
代数形式
max(7x+5y+4z)=
目的関数
制約条件式
5x+y+2z£20(1)
制約条件式
2x+2y+6z£30(2)
制約条件式
2x+6y+4z£40(3)
これらの制約条件式の他に暗黙にx≧0 ,y≧0 ,z≧0 が仮定されています。
このような課題が、線形計画法の代表例になります。
最大値の他に最小値も課題の対象です。
また制約条件式は通常≧または≦ですが、カルキングでは=の付いた制約条件式も含めます。
線形計画法に限り、上等号式 ≦ および ≧ に関しては、< または > で代用できます。
以下の例題ではそのような例題も含めています。
解き方
目的関数を含めて、選択します。
「実行《-「方程式関連《-「線形計画法《 で以下の線形計画法ダイアログ画面が出てきます。
OKボタンで以下のような結果が表示されます。
最大値
xの値
yの値
zの値
↓
↓
↓
↓
max(7x+5y+4z)={48.5714285714286, {2.85714285714286, 5.71428571428571, 0}}
5x+y+2z£20
2x+2y+6z£30
2x+6y+4z£40
この例のように数式は必ず、1次式です。上記(1),(2),(3)は標準形の式をしていますが、
カルキングでは1次式である限り、このような標準形でなくとも解くことができます。
標準形でない形式でも解けます
max(5(x+y+z)+2x-z)={48.5714285714286, {2.85714285714286, 5.71428571428571, 0}}
5x+y+2z£20
2
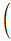
x+y+
z-5
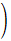
+3z
£20
2x+6y+4z£40
分数解の例
線形計画法ダイアログ画面で分数モードをチェックすると、分数解も得られます。
5x+y+2z<20
2x+2y+6z<30
2x+6y+4z<40
表形式では必ず標準形の係数を表にセットする必要があります。
表形式
sample
| max case |
|
|
|
|
|
| objective function |
7 |
5 |
4 |
= |
|
| constraint |
5 |
1 |
2 |
< |
20 |
| constraint |
2 |
2 |
6 |
< |
30 |
| constraint |
2 |
6 |
4 |
< |
40 |
この表は「入力《*「表/行列《-「線形計画法の諸元表《で作成します。
線形計画法では、最大、最少値の他に、各変数の値も同時に求めます。これらの値が
どこに表示されるかは、具体的に解いてみればすぐに判明します。
解き方
表を選択します。
「実行《-「方程式関連《-「円形計画法《 で以下の線形計画法ダイアログ画面が出てきます。
ここからは代数形式と同じ解き方になります。ここでは分数解を求めてみます。
最少ケース
線形計画の諸元表作成の時に「最少を求める《にチェックして表を作成します。
制約条件の上等号の混在のケースを求めてみます。解き方はいままでと同様です。
table2
| min case |
|
|
|
|
| objective function |
1 |
2 |
= |
|
| constraint |
1 |
1 |
£ |
3 |
| constraint |
1 |
1.1 |
³ |
2 |
| constraint |
-1 |
1 |
£ |
1 |
| constraint |
-1 |
1.1 |
³ |
0 |
計算結果
| min case |
1 |
0.909091 |
|
|
| objective function |
1 |
2 |
= |
2.81818 |
| constraint |
1 |
1 |
£ |
3 |
| constraint |
1 |
1.1 |
³ |
2 |
| constraint |
-1 |
1 |
£ |
1 |
| constraint |
-1 |
1.1 |
³ |
0 |



