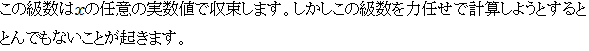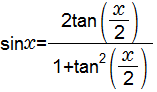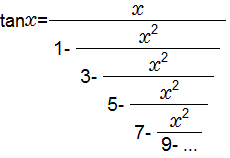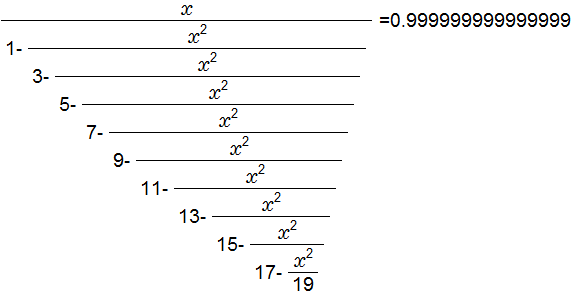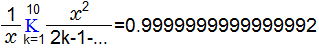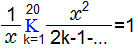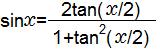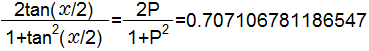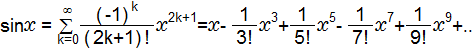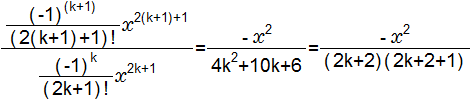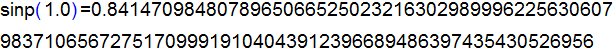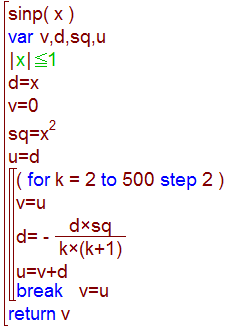三角関数の計算に関する話題

最も重要な数学関数の一つである三角関数はどのように計算されるのでしょうか。
今日の計算機の状況に沿って説明いたします。

Intelのx86アーキテクチャの計算機では、15桁の計算は、直接MPUチップで計算されています。
これは半導体生産技術の進歩により可能になったものですが、8ビットMPUの時代では、
三角関数のようなものは演算コプロセッサという別の半導体チップで計算されていました。

これらで採用されている計算アルゴリズムはCORDIC法といわれ、数表と漸化式で構成されて
います。この方法の重要な特徴は、加減算とビットシフト演算だけで計算可能という点で、特に
利用可能な機能が限定されたハードウエアの実装に適した方法です。
カルキングでは1000桁までの計算が可能ですが、 Intelのx86アーキテクチャの計算機では
このような高精度演算機能はありません。従ってソフトウエアプログラムで実現しています。

本解説ではCORDIC法の解説は割愛させていただき、主に微積分の公式を利用した方法の
解説をしたいと思います。ここではアイデアの本質の解説に力点を置き、重要ではありますが
細かな事項は省略いたします。

三角関数全体ではなくsin関数に焦点を絞って解説します。

sin関数はテーラー展開で知られていますが、無限級数の多項式で定義されています。

の時

したがって、sin関数を単純にテーラー展開して計算することは適切ではありません。
しかし幸いなことに、sin関数には周期性があります。
このためsin関数の計算アルゴリズムは比較的易しいと言えます。
しかしベッセル関数をはじめ多くの数学関数にはこのような美しい周期性の公式はありません。　
このような場合は特別の工夫が必要です。

この時の近似多項式（計算精度が10桁程度の時に適しています。）

以下のように計算式を変形すると乗算の計算回数が大幅に減少します。

実際に計算してみましょう。

実際の値は

0.295520206664834

↑

１２桁まで合っています！

の時

の時

ただしｎは整数

の時

の時

この方法は高精度計算の時に適しています

別解１

ここでは説明を簡単にするために、計算精度が15桁程度として方式の説明をします。

以下の公式より、sin関数の値を求めるためには、tan関数を求めればいいことになります。　
従って、まずtan関数の計算に取り組みます。

公式１

公式２

tan関数の連分数展開

周期性公式

ここでｎは整数

さらに以下の公式により

この値が計算できればいいことになります。

このようにｘの値を狭めることは、tanの連分数計算の収束の速さを高めることになります。

ここでいよいよ面倒な連分数の計算になります。

一般にこのような連文数の計算は、プログラムを作成する必要があります。
カルキングでいえばfor文で作成します。

15桁精度で代入定義

カルキングで直接計算

この時の数学的に正確な値は１ですから、ほぼ期待通りになりました。

15桁精度で代入定義

15桁精度で計算

この方法の利点は、15ケタを超える高精度計算も簡単にできることです。
この時は連分数の段数の10の値を、もっと大きな値に変更する必要があります。

30桁精度で代入定義

30桁精度で計算

以上でtan関数の求め方が分かったので、目的のsin関数の計算を行います。

を利用します。

代入定義

計算

検算

この方法は高精度計算の時に適しています

別解２

テーラー展開の公式を利用します。

高速化の工夫は、隣り合わせの項の値の比が比較的簡単であることを利用しています。

スクリプトのプログラムを使わないようににしてきましたが、残念ながらここの方法では利用せざる
を得ません。

詳しい説明は省略しますが、このヒントをもとに作成したプログラムが以下のsinpという関数です。
このプログラムは総和の値が収束したときに計算を終了するようにしました。

したがって計算精度や、パラメータの値によって計算回数が異なります。
以下のプログラムは計算精度が1000桁に対応できています。

計算例

15桁計算

ループ回数　=　9

100桁計算

ループ回数　=　35

解説はここで終えますが、他にもいろいろな方法があり、カルキングを利用して、簡単に実験を
することができます。