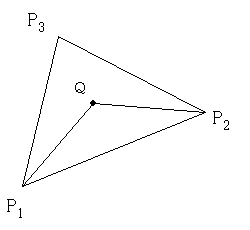
3角形に内接する円の導出
3角形の頂点の座標を指定して、3角形に内接する円を求める。
(1) 頂点を結ぶ直線の方程式を定める。
とすると,
(2) 直線に接する円の式
)から直線ax+by+c=0への距離をhとすれば、
それゆえ、直線ax+by+c=0に接する円の方程式を
とすれば,
求める円は3つの直線に接するので、
ここで
r>0
(3) 計算例
として、解を求めよう。
まず、直線式の係数に値を代入する。
次に、上の3つの接円の式とrの条件式を選択して、連立多項式を実行する。
そうすると、次の解を得る。
r = 3.574169848
r = 1.287516217
r = 5.607342525
r = 3.139063041
4組の解がある。これらの識別のため,次のように表記する。
これらの内、半径の最も小さい第2の解が、内接円に対応する。
他の3つは外接円に対応する。
【備考】
連立多項式の実行において、円の中心が3角形の内部にあるという条件を付加する
ことによって、解を内接円に限定してもよい。
r>0
中心点が3角形の
内部にある条件
>0
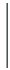
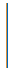
>0
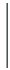
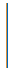
>0
上記の式を選択して、連立多項式を実行すると、
r = 1.287516217
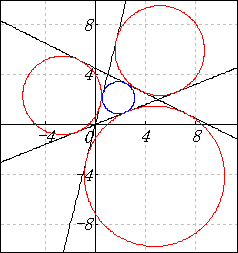
(4) 結果の図示
まず次式によって、3直線のグラフを書く。
次に、次式によって、円を書く。
下の図は、こうして得られたグラフである。
【別解法】
=
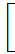
(tan
)+(tan
)
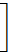
=
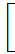
(tan
)+(tan
)
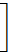
さらに
(3)
(1), (2), (3)を選択して,連立多項式を実行する。
連立多項式のダイアログでは、変数をx,yに指定する。
式(3)は次の理由で含めている。
が変数xのグループに属し、
が変数xのグループに属する。
それで、変数をx,yに指定すると、実質的な変数の個数は6つになる。
そこで、式(3)を追加して、方程式の個数を6つにしている。
こうして、次の解を得る。
x = 1.85979521725506
y = 2.13061549525983
そして
b=-1
とすると、半径rは次式で与えられる。
rの計算値は
r=1.28751622097121