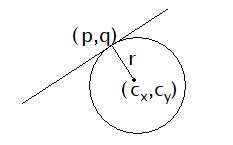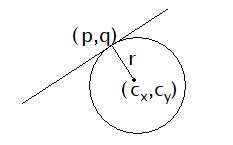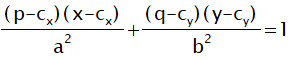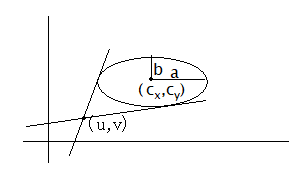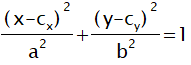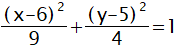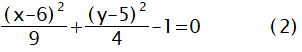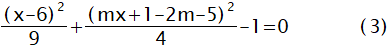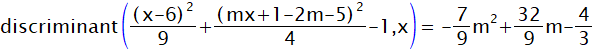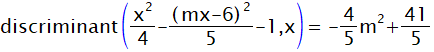二次曲線の接線とdiscriminant関数
二次曲線には楕円(円)、放物線、双曲線があります。
ここでは二次曲線の外の点から、二次曲線への接線を引く課題を解いてみましょう。
この課題に関しては、数学の公式がいくつか知られており、それらを使った解き方が、。
知られています。
この代表的な例
円に関しての公式
楕円の接線の公式
半径 r
今回の解説では、このような、二次曲線に関する
複数の接線の数学公式を使わずに、同じような
解き方で、接線の課題を解決します。
カルキングVer12とカルキング365でサポートされているdiscriminant関数を利用します。
これは2次方程式の判別式を求める関数です。
ここで説明する方法は、筆算でも当然実行可能です。
●円や楕円のケース
楕円の式
接線の式
y=mx+d
定数値の定義
この定義により
楕円と接線は以下のようになる。
楕円の式を以下のように変形する。
直線が楕円と交わるときは、通常2点である。接線の時のみ1点になる。
交点を求めるために、(1)のyを(2)式に代入する。
ここで(3)式の判別式を求める。discriminant関数は代数計算を使います。
方程式
を満たすmの値が、接線の勾配になる。
このmの方程式の解は以下のように求まる。
m = 4.15926814980057
m = 0.412160421628
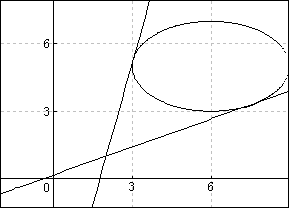
接線の二つの式が確定したので、楕円と二つの式を関数グラフで描画します。
y=m1x+1-2m1
y=m2x+1-2m2
●放物線のケース
放物線の外の点の座標を以下とします。
この点からの放物線への接線の式を
以下とする。
y=mx+n
この直線は(5)の点を通るため、以下の式を満たします。
-6=n
nの値が求まったため、接線の式は以下となります。
(4)式を変形すると、以下の式が得られます。
(7)式に(6)式のyを代入すると以下の式が得られます。
この式の判別式を計算します。
接戦になる条件は
従って
m=2
m=-2
m3,m4定数を以下のようにします。
(6)式から、接線式が確定し、以下のようになります。
y=2x-6
y=-2x-6
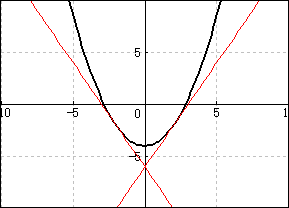
以上で、放物線の関数グラフが描画できます。
●双曲線のケース
外部の点の座標を、以下とします。
この点を通る直線の式は以下となります。
(8)式を変形すると以下の式が得られます。
(9)式のyを(10)式の代入する。
式(11)の変別式を求める。
方程式
の解は
m = -3.20156211871642
定数m5,m6を導入します。
これにより双曲線の二つ接線の式が得られました。
y=m5x - 6
y=m6x - 6
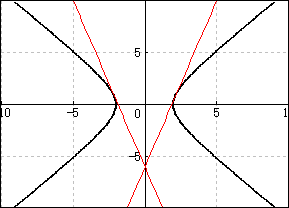
以上により、双曲線への二つの接線の描画ができます。