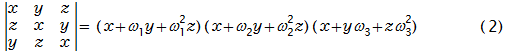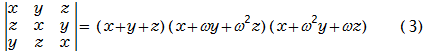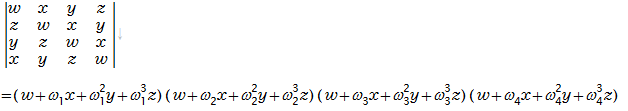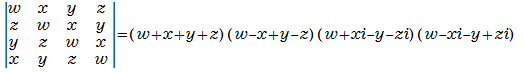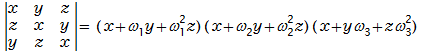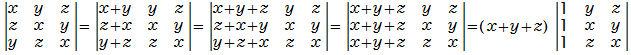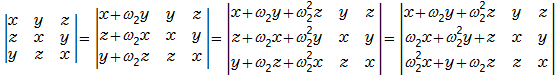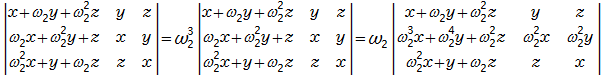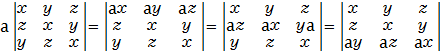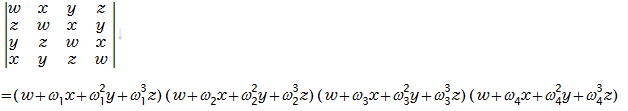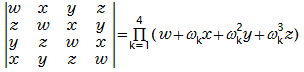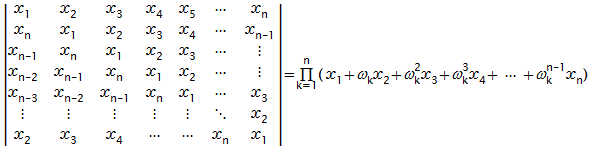k = 1, 2, 3,.. n

●3次巡回行列式の複素係数の因数分解

求め方は後で説明します。

ただし

k = 1, 2, 3

ただし

●４次巡回行列式の複素係数の因数分解

求め方は後で説明します。

ただし

k = 1, 2, 3, 4

●３次巡回行列式の複素係数の因数分解の解法

以下の因数分解を求める方法は、3つの因数があることを示します。

行列の法則から

　

行列の法則から

ここで

k = 1, 2, 3

従って

従って以下のように変形できます。

上記の式の変形は以下の行列の法則を適用しています。

以上は3次の巡回行列式ですが、同じように4次巡回行列式に関しても同じ方法で

以下の等式を証明できます。

k = 1, 2, 3,4

k = 1, 2, 3,4

以上は4次の巡回行列式ですが、同じようにｎ次巡回行列式に関しても同じ方法で

以下の等式を証明できます。

k = 1, 2, 3,.. n