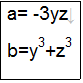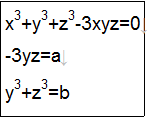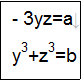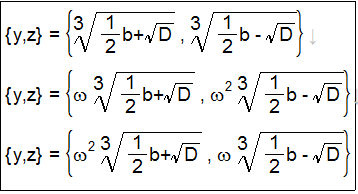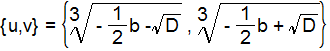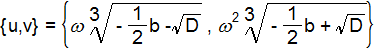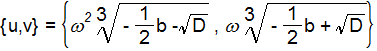解法シナリオ

以下の(2)が解ければ(1)が解ける

方程式(2)を解くシナリオ

●第一ステップ　因数分解の公式と式の変形に注目

式の変形

●第二ステップ　解くべき目標を転化する

(2)の方程式に代わって以下のようにx,y,zに関する連立3次方程式を解く

こちらを解く

この方程式の解と

（２）の方程式の解

のｘは同じになる。

●第三ステップ　未知数y,zに関する連立方程式の解を求める。

ただし

●第四ステップ　上記の第三ステップで求まるy,zを用いて以下の

　　ｘに関する3次方程式の解を求める。

従って、以下の2式が得られ、(3)ステップで得られるｙ、ｚを使いｘが求まる。

実は(4)を解く必要はありません。（実は(4)式を使っても同じ答えが出ます）

なぜなら、ステップ3で求まるｙ、ｚの解は3通りあり、これと(3)式を組み合わせ
ると、3通りのｘの解が求まります。

ここでｙ、ｚの符号を反転した補助変数のu,vを導入します。

u= - y

v= - z

こするとｘの3組の解は以下のようになります。

x= u+v

ここで、u,vはｙ、ｚの時と異なって、3乗根の中の符号が反転しています。