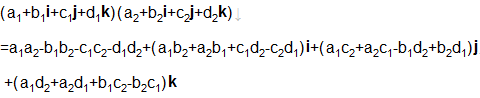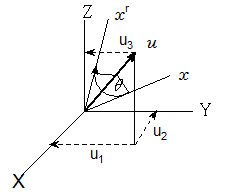a

実数

↓

行列表現

、

複素数

↓

a+b+c+d

、

行列表現

四元数

b+c+dは虚部

基底元,,に関しては次の式が定義されている。

定義

これらは定義より導ける。

四元数（quaternion（クォターニオン））は1843年にアイルランドの数学者ウィリアム・ローワン・ハミ
ルトンによって発明された。基本的考えは、複素数の拡張であり、複素数と異なり、掛け算の交換
則が成り立たない。まだベクトルが発明されていない時代にとってこれは驚くべきことでした。

大多数の読者にとって奇妙な四元数のトピックスを取り上げるのは、実用的観点と、行列の機能
の素晴らしさを鑑賞していただきたいためです。

実用的観点は、3次元における任意ベクトル方向で回転したときの座標点の求め方です。

多くの方のなじみのベクトル解析におけるこの解は、複雑な式になります。

しかし四元数では単純な式で求まります。

(1)実数で表される大きさ（ノルム）

複素数

四元数

a+b+c+dの大きさ

a-b-c-dはa+b+c+dの共軛と定義される。

(2)加減算

複素数と同じで、要素同士の加減算になる。

(3)ハミルトン積

　　おなじみのベクトルに関しては積は、内積と外積の二種類があります。四元数に関しての積は
　

ハミルトン積と言って一つです。　積が1つしかないことは複素数に似ています。

(4)ハミルトン積に関しての逆数

現在のカルキングはまだ四元数をサポートしていません。したがって、今まで使用してきたa + b
 + c + d　は計算には利用できません。

従って数式として認識で来る、4つの要素を持つ可変カッコを四元数の仮の表現とします。

この形はカルキングでベクトルになりますから、ベクトルの記法の計算式では四元数の計算には
なりません。　最も単純な方法は、行列表現を使う方法です。

四元数を行列表現して、行列形式で四元数計算をほとんどそのままの数式で計算できます。

計算が終わった後で、ベクトル表記に戻せば完了です！

ここでの表現規約

ベクトル形式での四元数の変数をギリシャ文字の小文字、四元数の変数はqを使います。

関数定義

関数Mはベクトル形式の四元数を行列形式に変換する。

共役行列（conjugate）

関数定義

関数Mはベクトル形式の四元数を共役形式の行列に変換する。

関数定義

関数Vは行列形式の四元数をベクトル形式に変換する。

四元数を使わずに、通常のベクトル計算でこの問題を解くことはかなり面倒です。

しかし四元数ではこの課題は単純な数式で求まります。

ただし

従って

この場合答えは、x軸上に移動する。

計算プロパティーはいずれも複素数モードとする。

代数代入定義

行列形式に変換

代数代入定義

代数代入定義

行列形式に変換

行列形式に変換

代数代入定義

行列形式での四元数計算

代数代入定義

代数代入定義

行列形式からベクトル形式への変換

代数計算

今回の計算例は、通常使われる数値計算モードで計算します。

代入定義

行列形式に変換

代入定義

代入定義

行列形式に変換

代入定義

行列形式に変換

行列形式での計算

代入定義

代入定義

行列形式からベクトル形
式への変換

計算